index.html

＜計算0＞　　u[0,T]=f[T], u[1,T]=-d/dT u[1,T]

＜計算1＞　初期分布=0、表面濃度＝（一定）の場合。　u[0,T]=0, u[1,T]=-d/dT u[1,T], u[X,0]=(const)

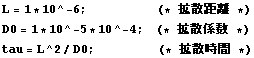
L = 1 * 10^-6 ; &nbs ... p; (* 拡散時間 *)

F[X_] := 0 ; & ... nbsp;カルシウムイオン濃度 NCa[X, T] の計算 ************)

NCa[X_, T_] = N0 * (1 - L * S2/(1 + L * S2) * X) + Sum[a[[n]] * Sin[ramda[[n]] * X] * Exp[-r ... p; 右端でのカルシウムイオンの流速 ************)

fluxCa[T_] = flux[1, T] ;

(*** ** ** ** ** ** 計算結果の表示 ************)

[Graphics:HTMLFiles/index_28.gif]

[Graphics:HTMLFiles/index_29.gif]

[Graphics:HTMLFiles/index_33.gif]

＜計算2＞　初期分布=（直線）、表面濃度＝0 の場合。　u[0,T]=1, u[1,T]=-d/dT u[1,T], u[X,0]=(const)

L = 1 * 10^-6 ; &nbs ... p; (* 拡散時間 *)

F[X_] := -0.5 * X + 1 ; &n ... nbsp;カルシウムイオン濃度 NCa[X, T] の計算 ************)

NCa[X_, T_] = N0 * (1 - L * S2/(1 + L * S2) * X) + Sum[a[[n]] * Sin[ramda[[n]] * X] * Exp[-r ... p; 右端でのカルシウムイオンの流速 ************)

fluxCa[T_] = flux[1, T] ;

(*** ** ** ** ** ** 計算結果の表示 ************)

[Graphics:HTMLFiles/index_45.gif]

[Graphics:HTMLFiles/index_46.gif]

[Graphics:HTMLFiles/index_48.gif]

$Plot[f[t], {t, 0, 1.*10^-7}]$

[Graphics:HTMLFiles/index_55.gif]

${t -> 1.*10^-8}$

$Plot[f[t], {t, 0, 2.*10^-8}]$

[Graphics:HTMLFiles/index_66.gif]

[Graphics:HTMLFiles/index_69.gif]

Created by Mathematica (July 18, 2007)