<例題1>
2点
A
(
3
,
4
)
,
B
(
5
,
-
2
)
を直径の両端とする円の方程式を求めよ。
解答例:
:直径
A
B
の中点が円の中心になる.中心の座標を求めると,
(
3
+
5
2
,
4
+
(
-
2
)
2
)
=
(
4
,
1
)
よって,
(
x
-
4
)
2
+
(
y
-
1
)
2
=
r
2
とおける.点
A
(
3
,
4
)
を通るので,
(
3
-
4
)
2
+
(
4
-
1
)
2
=
r
2
より,
r
2
=
10
よって,
(
x
-
4
)
2
+
(
y
-
1
)
2
=
10
.
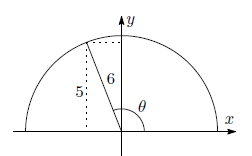
<例題2>第2象限の角
θ
に対して,
sin
θ
=
5
6
である.
cos
θ
と
tan
θ
の値を求めよ.
解答例:
sin
2
θ
+
cos
2
θ
=
1
より,
cos
2
θ
=
1
-
25
36
=
11
36
θ
は第2象限の角だから,
cos
θ
<
0
.
よって,
cos
θ
=
-
11
6
tan
θ
=
sin
θ
cos
θ
より,
tan
θ
=
5
6
-
11
6
=
-
5
11
<例題3>△ABCで
a
=
6
,
b
=
2
3
,
c
=
3
+
3
のとき,∠
A
を求めよ.
解答例:
余弦定理
a
2
=
b
2
+
c
2
-
2
b
c
cos
A
に代入して
6
=
12
+
9
+
6
3
+
3
-
4
3
(
3
+
3
)
cos
A
4
3
(
3
+
3
)
cos
A
=
18
+
6
3
したがって,
cos
A
=
18
+
6
3
4
3
(
3
+
3
)
=
6
(
3
+
3
)
4
3
(
3
+
3
)
=
3
2
3
=
3
2
0
<
A
<
π
より,
A
=
π
6

