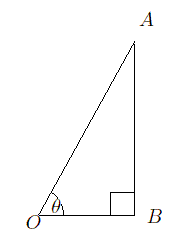
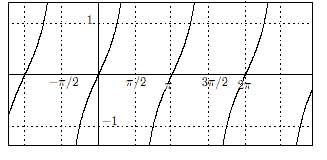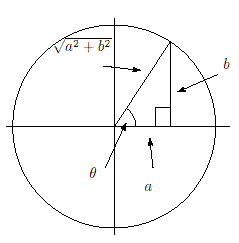三角比の定義
次の直角三角形で、
cos
θ
=
O
B
O
A
,
sin
θ
=
A
B
O
A
,
tan
θ
=
A
B
O
B
と定義する。
また、
O
A
cos
θ
=
O
B
,
O
A
sin
θ
=
A
B
もよく使われる関係式である。
三角関数の基本公式
tan
θ
=
sin
θ
cos
θ
cos
2
θ
+
sin
2
θ
=
1
sin
(
90
o
-
θ
)
=
cos
θ
,
cos
(
90
o
-
θ
)
=
sin
θ
1
+
tan
2
θ
=
1
cos
2
θ
三角比の拡張
0
≦
θ
≦
90
o
のときの三角比は次のように考えた。
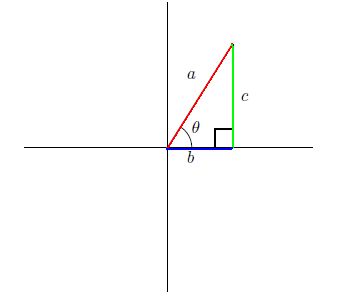
下のように
a
,
b
,
c
を取るときに、
sin
θ
=
c
a
,
cos
θ
=
b
a
,
tan
θ
=
c
b
.
θ
≧
90
o
のときは次のように長さ
a
の赤の線が原点の周りを回ると考える。この赤の線を動径と言う。
90
o
≦
θ
≦
180
o
としよう。
次の図のように考える。
a
,
b
,
c
を図のように取る。
このとき常に
a
>
0
とするが
b
は
x
軸の負の部分にあると考え
b
<
0
と考える。また、
c
は、
y
軸の正の部分にあると考え
c
>
0
と考える。三角比は同様に
sin
θ
=
c
a
,
cos
θ
=
b
a
,
tan
θ
=
c
b
.
と考える。
またこの場合道径は、第2象限を指しているので、第2象限の角という言い方をする。
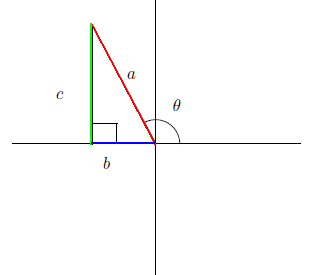
180
o
≦
θ
≦
270
o
としよう。
次の図のように考える。
a
,
b
,
c
を図のように取る。
このとき常に
a
>
0
とするが
b
は
x
軸の負の部分にあると考え
b
<
0
と考える。また、
c
も、
y
軸の負の部分にあるので
c
<
0
と考える。三角比は同様に
sin
θ
=
c
a
,
cos
θ
=
b
a
,
tan
θ
=
c
b
.
とする。またこの場合道径は、第3象限を指しているので、第3象限の角という言い方をする。
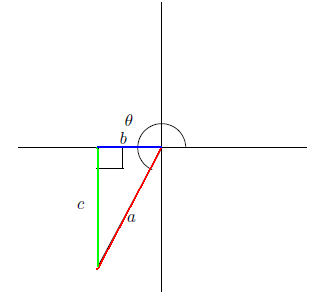
270
o
≦
θ
≦
360
o
としよう。
次の図のように考える。
a
,
b
,
c
を図のように取る。
このとき常に
a
>
0
とするが
b
は
x
軸の正の部分にあるので
b
>
0
と考える。また、
c
は、
y
軸の負の部分にあるので
c
<
0
と考える。三角比は同様に
sin
θ
=
c
a
,
cos
θ
=
b
a
,
tan
θ
=
c
b
.
とする。またこの場合道径は、第4象限を指しているので、第4象限の角という言い方をする。
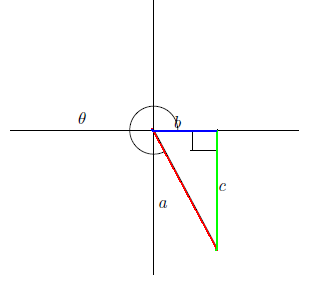
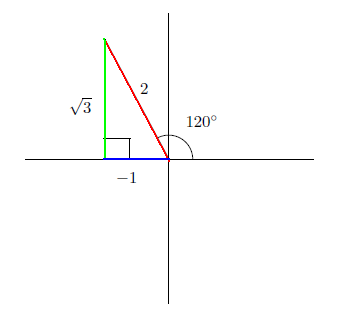
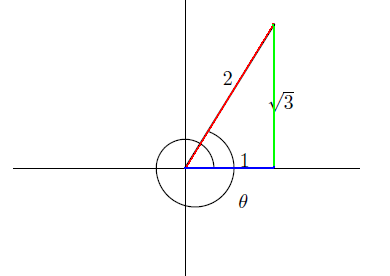
例1
θ
=
120
o
とする。すると次のような図になる。
従って
sin
θ
=
3
2
,
cos
θ
=
-
1
2
,
tan
θ
=
-
3
.
a
=
2
とする。
b
<
0
であるので
b
=
-
1
。
c
>
0
であるので
c
=
3
。
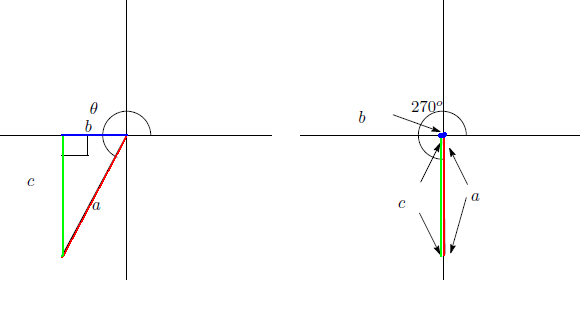
例2
θ
=
270
o
とする。第3象限の角であれば次の左の図のようになるが
θ
=
270
o
のときは下の右側の図になる。この場合
a
=
1
とすると
b
=
0
,
c
=
-
1
となる。従って
sin
θ
=
-
1
1
=
-1
,
cos
θ
=
0
1
=
0
,
tan
θ
=
-
1
0
=
×
.
一般角の三角比
θ
≧
360
o
の角を次のように考える。
例えば
θ
=
420
o
を
420
o
=
360
o
+
60
o
と思い、
420
o
=
一周
+
60
o
とする。すなわち次の図のように考える。
この場合三角比は
60
o
と同じとする。
すなわち
sin
420
o
=
sin
60
o
=
3
2
,
cos
420
o
=
cos
60
o
=
1
2
,
tan
420
o
=
tan
60
o
=
3
,
まとめると
θ
≧
360
o
の場合、
θ
=
n
×
360
o
+
a
とする。
ここで
n
は自然数で、
0
≦
a
≦
360
o
。
θ
は動径が
n
周原点をまわり、さらに
a
度回転したものと思う。
θ
<
0
の角は動径が、時計回りに回転すると考える。
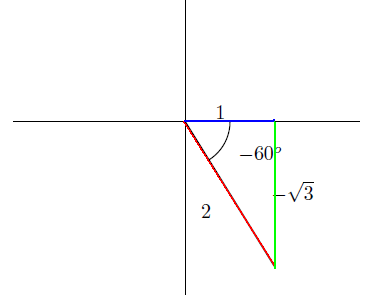
例えば
θ
=
-
60
o
の場合は、図のようになる。
またこの場合三角比は
300
o
と同じとなる。すなわち
sin
(
-
60
o
)
=
sin
300
o
=
-
3
2
,
cos
(
-
60
o
)
=
cos
300
o
=
1
2
,
tan
(
-
60
o
)
=
tan
300
o
=
-
3
,
このように
0
o
≦
θ
≦
360
o
以外の角まで範囲を広げた角度を一般角という。
弧度法
直角は
90
o
というようなはかり方を今までしてきたが、このような角度の単位を六十分法という。
今回は弧度法という六十分法とは別の角度のはかり方を学習しよう。
弧度法の方が、数学的に自然であり、数学や工学では、
主に弧度法が使われている。
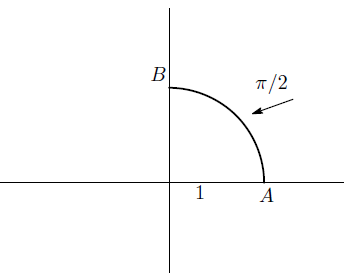
下の図で、この角度を測ることを考える。
O
を中心に半径
1
の円を描き
弧
A
B
の長さをこの角の大きさとする。
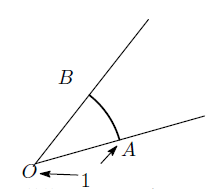
単位としてラジアンを使う。
例えば六十分法での
90
o
は、図のように弧
A
B
の長さであるので
π
2
ラジアンとなる。
六十分法での
t
o
をラジアンで表してみよう。
上記のように
90
o
のときは
π
2
ラジアンであるので
t
o
のとき
θ
ラジアンとすると
t
o
:
θ
=
90
o
:
π
2
。すなわち
90
θ
=
π
t
2
。よって
θ
=
π
t
180
。
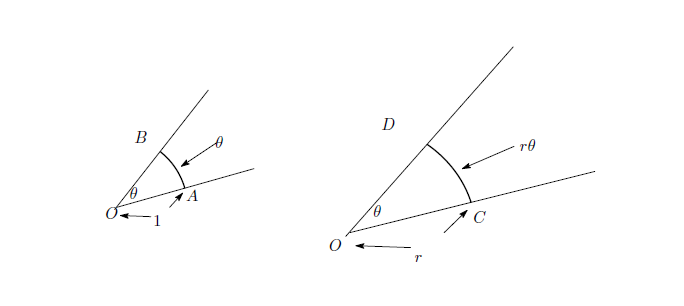
弧の長さと扇形の面積
中心角が
θ
で、半径が
r
ある扇形の弧の長さを求めてみよう。
下の図のように中心角が
θ
であるので、半径
1
に対する弧の
長さが
θ
になる。次の2つの扇形は相似である。従って
半径が
r
のときの弧の長さは半径が
1
のときの弧の長さの
r
倍
であるので弧の長さは
r
θ
になる。
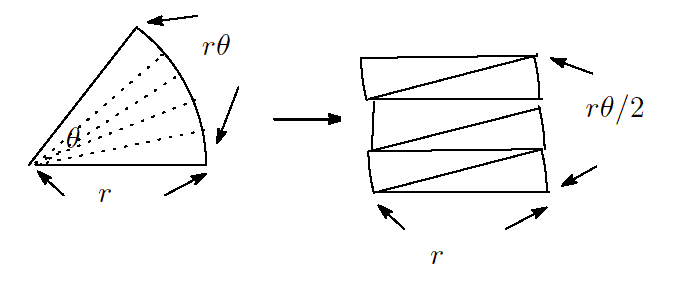
次に、この扇形の面積を求めてみよう。中学校で習ったような、
円のときを考えて中心角に比例することを使って導く方法が
よく使われるが、次の導き方を紹介しよう。
次の図のように、扇形を薄く切っていく。そして互い違いに
右の図のように積み上げていく。するとおおよそ、長方形に
なる。横が
r
で高さが扇形の弧の長さの半分すなわち
r
θ
2
であるので、面積は
r
2
θ
2
となる。
例:半径が
3
で中心角が
π
4
の扇形の面積。
3
2
π
4
2
=
9
π
8
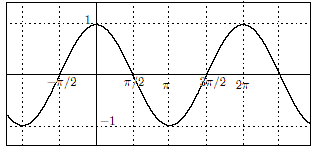
三角関数のグラフ
y
=
sin
x
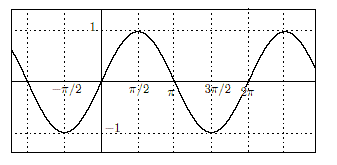
y
=
cos
x
y
=
tan
x
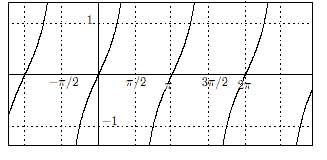
三角関数の公式
(1)基本公式
tan
θ
=
sin
θ
cos
θ
cos
2
θ
+
sin
2
θ
=
1
1
+
tan
2
θ
=
1
cos
2
θ
三角関数の加法公式
sin
(
x
+
y
)
=
sin
x
cos
y
+
cos
x
sin
y
sin
(
x
-
y
)
=
sin
x
cos
y
-
cos
x
sin
y
cos
(
x
+
y
)
=
cos
x
cos
y
-
sin
x
sin
y
cos
(
x
-
y
)
=
cos
x
cos
y
+
sin
x
sin
y
tan
(
x
+
y
)
=
tan
x
+
tan
y
1
-
tan
x
tan
y
tan
(
x
-
y
)
=
tan
x
-
tan
y
1
+
tan
x
tan
y
上記の三角関数の加法公式を証明してみよう。いろいろな証明法があるので挑戦してみるとよい。
下の図で∠
B
A
D
=
x
,∠
C
A
D
=
y
とする。
△
A
B
C
の面積は、後で述べる公式により
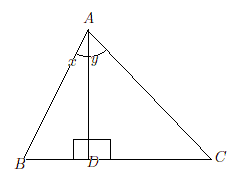
△
A
B
C
の面積
=
1
2
A
B
×
A
C
×
sin
∠
B
A
C
=
1
2
A
B
×
A
C
×
sin
(
x
+
y
)
.
一方、
A
D
=
A
B
cos
x
,
B
D
=
A
B
sin
x
,
A
D
=
A
C
cos
y
,
C
D
=
A
C
sin
y
となるので
△
A
B
D
の面積
=
1
2
A
D
×
B
D
=
1
2
A
B
sin
x
×
A
C
cos
y
=
1
2
A
B
×
A
C
sin
x
cos
y
同様にして△
A
C
D
の面積
=
1
2
A
B
×
A
C
cos
x
sin
y
従って
1
2
A
B
×
A
C
×
sin
(
x
+
y
)
=
1
2
A
B
×
A
C
sin
x
cos
y
+
1
2
A
B
×
A
C
cos
x
sin
y
1
2
A
B
×
A
C
で両辺を割って
sin
(
x
+
y
)
=
sin
x
cos
y
+
cos
x
sin
y
他の加法公式はこの公式から導くことができるので、試みてみよう。
三角関数の加法公式から導かれる公式
これらの公式は、覚えるより加法公式から導けるようにしておいた方がよい
(1)
sin
2
x
=
2
sin
x
cos
x
(2)
cos
2
x
=
cos
2
x
-
sin
2
x
=
2
cos
2
x
-
1
=
1
-
2
sin
2
x
(3)
cos
2
x
=
1
+
cos
2
x
2
(4)
sin
2
x
=
1
-
cos
2
x
2
(5)
sin
x
cos
y
=
sin
(
x
+
y
)
+
sin
(
x
-
y
)
2
(6)
cos
x
cos
y
=
cos
(
x
+
y
)
+
cos
(
x
-
y
)
2
(7)
sin
x
sin
y
=
-
(
cos
(
x
+
y
)
-
cos
(
x
-
y
)
)
2
(8)
sin
A
+
sin
B
=
2
sin
(
A
+
B
2
)
cos
(
A
-
B
2
)
(9)
cos
A
+
cos
B
=
2
cos
(
A
+
B
2
)
cos
(
A
-
B
2
)
(10)
cos
A
-
cos
B
=
-
2
sin
(
A
+
B
2
)
sin
(
A
-
B
2
)
三角関数の合成
合成公式。
a
sin
x
+
b
cos
x
=
a
2
+
b
2
sin
(
x
+
θ
)
ここで
cos
θ
=
a
a
2
+
b
2
,
sin
θ
=
b
a
2
+
b
2
証明
a
sin
x
+
b
cos
x
=
a
2
+
b
2
(
a
a
2
+
b
2
×
sin
x
+
b
a
2
+
b
2
×
cos
x
)
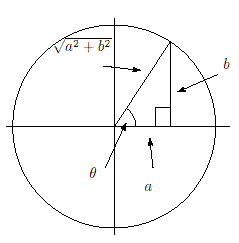
上の図のように
θ
をとると
cos
θ
=
a
a
2
+
b
2
sin
θ
=
b
a
2
+
b
2
a
2
+
b
2
(
a
a
2
+
b
2
×
sin
x
+
b
a
2
+
b
2
×
cos
x
)
=
a
2
+
b
2
(
sin
x
cos
θ
+
cos
x
sin
θ
)
加法公式を使って
=
a
2
+
b
2
sin
(
x
+
θ
)
三角形と三角関数
正弦定理
△
A
B
C
で,
a
=
C
B
,
b
=
A
C
,
c
=
A
B
とする。
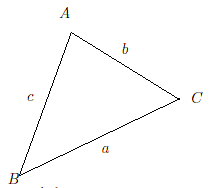
このとき
a
sin
A
=
b
sin
B
=
c
sin
C
証明次の図のように、△
A
B
C
の外接円の中心を
O
とし、
O
から、
B
C
に降ろした垂線との交点を
D
とする。
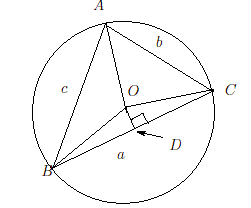
円周角と中心角の関係より、
∠
C
A
B
=
1
2
∠
C
O
B
=∠
C
O
D
従って、
C
O
sin
A
=
C
O
sin
∠
C
O
D
=
C
D
=
1
2
C
B
=
1
2
a
ここで、△
A
B
C
の外接円の半径を
r
とすると、
r
=
C
O
。従って、まとめると
r
sin
A
=
1
2
a
。すなわち
a
sin
A
=
2
r
。
同様にして
b
sin
B
=
2
r
,
c
sin
C
=
2
r
従って
a
sin
A
=
b
sin
B
=
c
sin
C
余弦定理
△
A
B
C
で,
a
=
C
B
,
b
=
A
C
,
c
=
A
B
とする。

このとき
a
2
=
b
2
+
c
2
-
2
b
c
cos
A
b
2
=
c
2
+
a
2
-
2
c
a
cos
B
c
2
=
a
2
+
b
2
-
2
a
b
cos
C
証明次の図のように、各頂点から垂線を下ろす。また図のように各辺を1辺とする正方形を描く。
すると
長方形
E
C
P
V
の面積
=
長方形
C
D
X
U
の面積,
長方形
B
F
W
S
の面積
=
長方形
B
D
X
T
の面積,
長方形
A
F
W
R
の面積
=
長方形
A
E
V
Q
の面積,
証明は、三平方の定理でよく使われる証明方法と同じ方法で証明できる。
各自証明してみよう。
従って
正方形
B
T
U
C
の面積
=
長方形
B
F
W
S
の面積
+
長方形
E
C
P
V
の面積
=正方形
B
S
R
A
の面積
+
正方形
A
C
P
Q
の面積
-
長方形
A
F
W
R
の面積
=
長方形
A
E
V
Q
の面積
ここで正方形
B
T
U
C
の面積
=
a
2
,正方形
B
S
R
A
の面積
=
c
2
,正方形
A
C
P
Q
の面積
=
b
2
,
長方形
A
F
W
R
の面積
=
b
c
cos
A
,長方形
A
E
V
Q
の面積
=
b
c
cos
A
であるので、
a
2
=
b
2
+
c
2
-
2
b
c
cos
A
を得る。