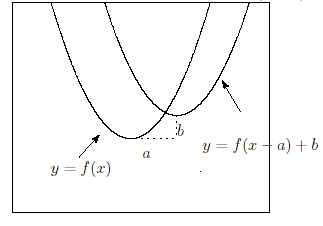
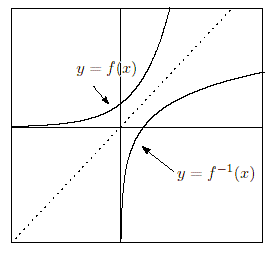関数のグラフの平行移動
関数
y
=
f
(
x
)
のグラフを
x
軸と平行に
a
だけ平行移動し、
y
軸と平行に
b
だけ平行移動したものは、関数
y
=
f
(
x
-
a
)
+
b
のグラフとなる。
例:
y
=
x
2
+
2
x
のグラフを
x
軸と平行に
3
だけ平行移動し、
y
軸と平行に
-
1
だけ平行移動したものは
y
=
(
x
-
3
)
2
+
2
(
x
-
3
)
+
1
のグラフとなる。
逆関数
関数
y
=
f
(
x
)
に対して、変数
y
から
x
への対応があるときそれを元の関数の逆関数と言う。具体的に対応を与える式を求めることをその逆関数を求めるという。
y
=
f
(
x
)
の逆関数を
x
=
f
-
1
(
y
)
と記す。通常、
x
=
f
-
1
(
y
)
で
x
と
y
を入れかえるので、
y
=
f
-
1
(
x
)
と記す。
例1:
y
=
2
x
+
1
のとき、
x
を
y
の式で書くと
x
=
y
-
1
2
。
従って
y
=
2
x
+
1
の逆関数は
y
=
x
-
1
2
。例2:
y
=
x
2
のとき、
x
を
y
の式で書くと
x
=
±
y
。
従って
y
の値に対して一般的に2通りの
x
が対応するので(ひとつに決まらないという意味で)逆関数は、存在しない。
逆関数のグラフ
関数
y
=
f
(
x
)
のグラフとその逆関数
y
=
f
-
1
(
x
)
のグラフは直線
y
=
x
に対して対称である。
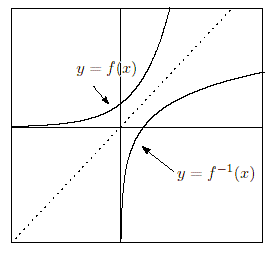
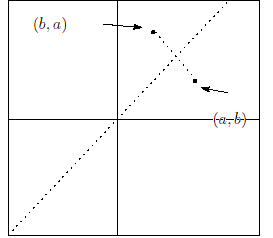
上記の理由:関数
y
=
f
(
x
)
で
x
=
a
のとき
y
=
b
であるとしよう。その逆関数
y
=
f
-
1
(
x
)
で考えると
x
=
b
のとき
y
=
a
となる。すなわち関数
y
=
f
(
x
)
のグラフ上に点
(
a
,
b
)
があるとき逆関数
y
=
f
-
1
(
x
)
のグラフ上に点
(
b
,
a
)
がある。点
(
a
,
b
)
と点
(
b
,
a
)
とは直線
y
=
x
に対して対称であるので関数
y
=
f
(
x
)
のグラフとその逆関数
y
=
f
-
1
(
x
)
のグラフは直線
y
=
x
に対して対称となる。
対数関数
a
>
0
としまた
a
≠
1
。今
a
q
=
p
という関係があったとする。
このとき
q
=
log
a
p
と記すことにする。
すなわち
y
=
a
x
と
y
=
log
a
x
とは逆関数同士の関係である。
例:
2
3
=
8
より
log
2
8
=
3
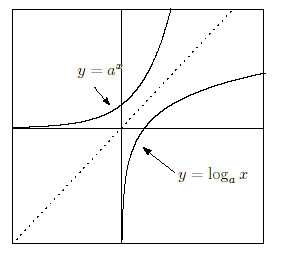
対数関数のグラフ
y
=
a
x
と
y
=
log
a
x
とは逆関数同士の関係であるのでグラフは直線
y
=
x
に対して対称となる。
1
<
a
のとき
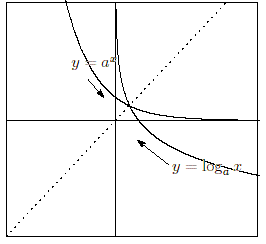
0
<
a
<
1
のとき
対数関数の公式
(0)
log
a
1
=
0
,
log
a
a
=
1
(1)
log
a
p
q
=
log
a
p
+
log
a
q
(2)
log
a
p
q
=
log
a
p
-
log
a
q
(3)
log
a
p
c
=
c
log
a
p
(4)
log
a
p
=
log
c
p
log
c
a
,(底の変換公式)