2次関数の定義
a
,
b
,
c
を定数としたとき、
y
=
a
x
2
+
b
x
+
c
を2次関数という。
2次関数のグラフ
放物線と呼ばれる。
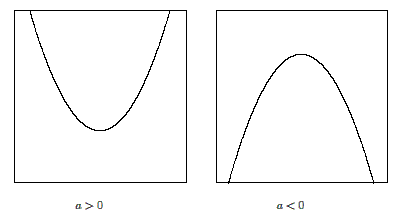
a
>
0
のときは上に開いているグラフ(下に凸ともいう)
a
<
0
のときは下に開いているグラフ(上に凸ともいう)になる。
2次関数の標準形
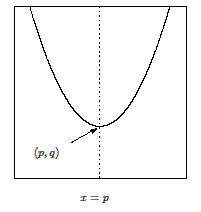
y
=
a
(
x
-
p
)
2
+
q
を標準形という。
(
p
,
q
)
はこの関数のグラフの頂点と呼ばれる。
また、軸は直線
x
=
p
となる。
グラフは軸に関して対称となる。
また
y
=
a
x
2
のグラフを
x
方向に
p
y
方向に
q
平行移動して得られる。
標準形への変形
y
=
a
x
2
+
b
x
+
c
y
=
a
(
x
2
+
b
x
a
)
+
c
y
=
a
(
(
x
+
b
2
a
)
2
-
(
b
2
a
)
2
)
+
c
y
=
a
(
x
+
b
2
a
)
2
-
b
2
4
a
+
c
y
=
a
(
x
+
b
2
a
)
2
-
b
2
-
4
a
c
4
a
方程式と不等式
方程式とは
1変数の
n
次代数方程式とは
a
n
x
n
+
a
n
-
1
x
n
-
1
+
...
+
a
0
=
0
のことである。
a
n
,
a
n
-
1
,...,
a
0
は係数と呼ばれ、
一般的には実数であるが、通常有理数ないしは、整数で考える。
例えば、
x
2
-
2
=
0
は2次方程式である。
方程式の解
方程式
a
n
x
n
+
a
n
-
1
x
n
-
1
+
...
+
a
0
=
0
の
x
にある数を代入してこの式が成立するとき
この数をこの方程式の解または、根と言う。
例えば、方程式
x
2
-
2
=
0
の解は
2
と
-
2
である。
どのような方程式にも解が存在していることが知られている。ただし
このときの解は複素数になる。(実数も複素数の一部です)。
これは代数学の基本定理と言われています。ドイツの数学者のガウス
が得たものです。
方程式の解の公式
2次方程式
a
x
2
+
b
x
+
c
=
0
の解を与える公式を導いてみましょう。
a
x
2
+
b
x
+
c
=
0
a
(
x
2
+
b
a
x
)
+
c
=
0
a
(
(
x
+
b
2
a
)
2
-
(
b
2
a
)
2
)
+
c
=
0
(
x
+
b
2
a
)
2
-
(
b
2
a
)
2
=
-
c
a
(
x
+
b
2
a
)
2
=
(
b
2
a
)
2
-
c
a
(
x
+
b
2
a
)
2
=
b
2
-
4
a
c
4
a
2
x
+
b
2
a
=
±
b
2
-
4
a
c
2
a
x
=
-
b
±
b
2
-
4
a
c
2
a
この解の公式より、
b
2
-
4
a
c
の符号により実数解の個数などが分かる。
すなわち、
b
2
-
4
a
c
>
0
のとき、2次方程式
a
x
2
+
b
x
+
c
=
0
は異なる2つの実数解を持つ。
b
2
-
4
a
c
=
0
のとき、2次方程式
a
x
2
+
b
x
+
c
=
0
は1つの実数解を持つ。このとき重解を持つという。
b
2
-
4
a
c
<
0
のとき、2次方程式
a
x
2
+
b
x
+
c
=
0
は実数解を持たない。ただし異なる2つの虚数解を持つ。
b
2
-
4
a
c
は2次方程式
a
x
2
+
b
x
+
c
=
0
の判別式と呼ばれる。
3次方程式
a
x
3
+
b
x
2
+
c
x
+
d
=
0
の解を与える公式も同様にして
与えられるが、かなり巧妙な変形を必要とする。
イタリアのCardano(カルダノ)による公式が知られている。興味のある人は
岐阜高専の岡田先生のホームページ()に良い解説
があるので参照してみると良い。4次方程式の解も
Cardano(カルダノ)の弟子のFerrariによって発見された。ただ、これらの公式の第一発見者をめぐっては議論があるようである。
5次以上の解の公式は存在しないことが、Abel(アーベル)
によって証明された。ただし解の公式は2次方程式の解の公式
のように根号と代数記号を使って表されるもののみを考える。
またAbel(アーベル)と同時代のガロアは方程式の代数的な理論を
発展させた。ガロアの理論は、数学の代数と呼ばれる分野の基礎理論となった。
剰余の定理と因数定理
p
(
x
)
を変数
x
の多項式とする。
a
を定数とし、
p
(
x
)
を
x
-
a
で割った
ときの余りは
p
(
a
)
で与えられることが知られている。これを剰余の定理
と呼ぶ。例えば
x
3
-
2
を
x
-
2
で割ったらその余りは
2
3
-
2
=
6
となる。
剰余の定理をざっと証明しよう。
p
(
x
)
を
x
-
a
で割った余りを
r
(
x
)
とする。また、商を
q
(
x
)
とする。すると
p
(
x
)
=
q
(
x
)
(
x
-
a
)
+
r
(
x
)
となる。
r
(
x
)
の次数は
x
-
a
の次数よりすくないはずである。
従って
r
(
x
)
の次数は
0
次になるはずであるので、
r
(
x
)
は定数になる。
r
(
x
)
=
c
とおく。ここで、
x
=
a
を代入すると、
p
(
a
)
=
q
(
a
)
(
a
-
a
)
+
c
。
p
(
a
)
=
c
となる。すなわち剰余の定理が証明されたことになる。
次に因数定理を説明しよう。
-------------------------------------------------------------
因数定理
p
(
x
)
を変数
x
の多項式とする。
a
を定数とし
p
(
a
)
=
0
のとき、
p
(
x
)
は
x
-
a
で割り切れる。すなわち
p
(
x
)
=
(
x
-
a
)
q
(
x
)
と書ける。ここで、
q
(
x
)
は
多項式である。
-------------------------------------------------------------
例えば、
x
3
+
2
x
2
-
9
x
+
2
に
x
=
2
を代入すると
2
3
+
2×2
2
-
9
×
2
+
2
=
0
となるので、
x
-
2
で割り切れる。実際、
x
3
+
2
x
2
-
9
x
+
2
=
(
x
-
2
)
(
x
2
+
4
x
-
1
)
この因数定理は、上記の剰余の定理から導くことができる。
2次不等式の解法
例えば
x
2
-
4
>
0
を満たす
x
の範囲を求めることを2次不等式を解くと
言う。解法として2次関数のグラフを考察する方法とや表を利用する
方法がある。まず2次関数のグラフを考察する方法から解説しよう。
x
2
-
4
>
0
を解く問題では
y
=
x
2
-
4
と置いてみる。するとグラフは
以下のようになる。
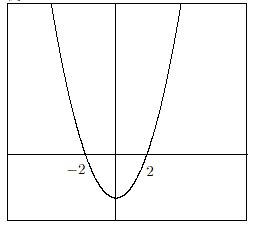
図に見るように
x
>
2
または
x
<
-
2
のときにのみ
y
>
0
となる。従って解は
x
>
2
または
x
<
-
2
となる。
次に
x
2
+
x
+
1
≧
0
を考えてみよう。
y
=
x
2
+
x
+
1
とおきグラフを
考察してみよう。
x
軸との交点は
x
2
+
x
+
1
=
0
の解であるがこの判別式
の値は
1
2
-
4
=
-
3
であるので、実数解は持たない。グラフは次のようになる。
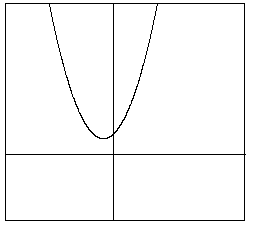
従って
x
2
+
x
+
1
≧
0
の解はすべての実数となる。まとめると次のようになる。
a
x
2
+
b
x
+
c
≧
0
の解は次のように場合わけされる。
D
=
b
2
-
4
a
c
とする。また
a
>
0
と仮定する。また、
α
,
β
を
a
x
2
+
b
x
+
c
=
0
の解とする。
(1)
D
>
0
のとき
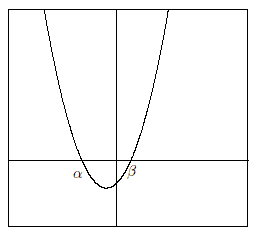
x
<
α
,
x
>
β
。ただし
α
<
β
。
(2)
D
=
0
のとき
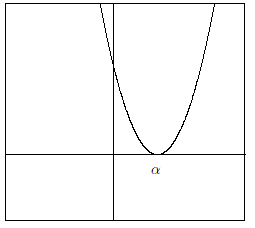
x
は全実数。
(3)
D
<
0
のとき

x
は全実数。
また表を使って解くことができる場合もある。例えば
(
x
-
1
)
(
x
+
2
)
>
0
を解いてみよう。
表を作ってみると
|
x
|
... |
-
2
|
... |
1
|
... |
|
x
+
2
|
-
|
0
|
+ |
+ |
+ |
|
x
-
1
|
-
|
-
|
-
|
0
|
+ |
|
(
x
-
1
)
(
x
+
2
)
|
+ |
0
|
-
|
0
|
+ |
この表より、
x
<
-
2
,
x
>
1
。
同様にして3次以上の不等式も因数分解できるときに解くことができる。
例えば、
(
x
+
2
)
(
x
-
1
)
(
x
+
2
)
≧
0
を解いてみよう。
表を作ると
|
x
|
... |
-
2
|
... |
1
|
... |
2
|
... |
|
x
+
2
|
-
|
0
|
+ |
+ |
+ |
+ |
+ |
|
x
-
1
|
-
|
-
|
-
|
0
|
+ |
+ |
+ |
|
x
-
2
|
-
|
-
|
-
|
-
|
-
|
0
|
+ |
|
(
x
+
2
)
(
x
-
1
)
(
x
+
2
)
|
-
|
0
|
+ |
0
|
-
|
0
|
+ |
以上より
-
2
≦
x
≦
1
,
2
≦
x
不等式の証明
例えば次の問題を考えてみよう。
-----------------------------------------------------------
(
a
2
+
b
2
)
(
x
2
+
y
2
)
≧
(
a
x
+
b
y
)
2
を証明し、等号が成立する場合を述べよ。
-----------------------------------------------------------
通常、大きい項-小さい項
≧
0
を示せばよい。
(
a
2
+
b
2
)
(
x
2
+
y
2
)
-
(
a
x
+
b
y
)
2
=
a
2
x
2
+
a
2
y
2
+
b
2
x
2
+
b
2
y
2
-
(
a
2
x
2
+
2
a
x
b
y
+
b
2
y
2
)
=
a
2
y
2
+
b
2
x
2
-
2
a
x
b
y
=
(
a
y
-
b
x
)
2
ここで最後の式は2乗しているのでもちろん
(
a
y
-
b
x
)
2
≧
0
。
従って
(
a
2
+
b
2
)
(
x
2
+
y
2
)
-
(
a
x
+
b
y
)
2
≧
0
すなわち
(
a
2
+
b
2
)
(
x
2
+
y
2
)
≧
(
a
x
+
b
y
)
2
また等号は
(
a
y
-
b
x
)
2
=
0
のときすなわち
a
y
-
b
x
=
0
のとき成立する。
次の不等式は相加平均
≧
相乗平均と呼ばれている不等式で
不等式の証明でよく利用される。
-----------------------------------------------------------
a
≧
0
,
b
≧
0
とする。
a
+
b
2
≧
a
b
が成立し、等号は
a
=
b
のときに限り成立する。
-----------------------------------------------------------
証明。
a
+
b
2
-
a
b
=
a
+
b
-
2
a
b
2
=
a
-
2
a
b
+
b
2
=
(
a
)
2
-
2
a
b
+
(
b
)
2
2
=
(
a
-
b
)
2
2
≧
0
.
一方、等号は上の式より
a
-
b
=
0
のときであるから、
a
=
b
のときに限り等号が成立する。
次は相加平均
≧
相乗平均の例である。
-----------------------------------------------------------
x
>
0
とする。
x
+
1
x
≧
2
を示しなさい。
-----------------------------------------------------------
相加平均
≧
相乗平均の公式
a
+
b
2
≧
a
b
で
a
=
x
,
b
=
1
x
を代入して
x
+
1
x
2
≧
x
×
1
x
,すなわち
x
+
1
x
2
≧
1
が成立する。
両辺に
2
をかけて、
x
+
1
x
≧
2
。また等号は
x
=
1
x
のときなので、
x
2
=
1
のとき成立する。
x
2
=
1
を
x
>
0
で解くと
x
=
1
。従って
x
=
1
のとき等号は成立する。








