<例題1>関数
f
(
x
)
=
x
3
を定義にしたがって微分せよ.
解答例:微分の定義式は,
f
'
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
-
f
(
x
)
h
f
(
x
+
h
)
-
f
(
x
)
=
(
x
+
h
)
3
-
x
3
=
3
x
2
h
+
3
x
h
2
+
h
3
=
h
(
3
x
2
+
3
x
h
+
h
2
)
f
'
(
x
)
=
lim
h
→
0
h
(
3
x
2
+
3
x
h
+
h
2
)
h
=
lim
h
→
0
(
3
x
2
+
3
x
h
+
h
2
)
=
3
x
2
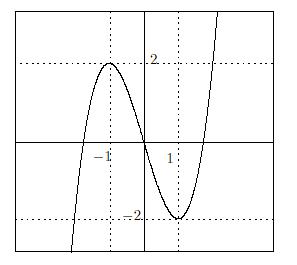
<例題2>:関数
y
=
x
3
-
3
x
の増減を調べて、そのグラフをかけ.
解答例:
f
(
x
)
=
x
3
-
3
x
とおくと、
f
'
(
x
)
=
3
x
2
-
3
=
3
(
x
2
-
1
)
=
3
(
x
+
1
)
(
x
-
1
)
より、
f
'
(
x
)
=
0
となる
x
の値は、
x
=
-
1
,
1
だから、増減表は
|
x
|
... |
-
1
|
... |
1
|
|
|
f
'
(
x
)
|
+ |
0 |
-
|
0 |
+ |
|
f
(
x
)
|
↗
|
極大 |
↘
|
極小 |
↗
|
極大値
f
(
-
1
)
=
(
-
1
)
3
-
3
×
(
-
1
)
=
2
,極小値
f
(
1
)
=
1
-
3
=
-
2
<例題3>:次の関数を微分しなさい.
(1)
y
=
1
2
x
+
1
(2)
y
=
e
-
x
2
(3)
y
=
x
2
log
x
(4)
y
=
cos
3
x
解答例:
(1)
u
=
2
x
+
1
とおくと、
y
=
1
u
1
2
=
u
-
1
2
y
'
=
-
1
2
u
-
3
2
×
d
u
d
x
=
-
1
2
(
2
x
+
1
)
-
3
2
×
2
=
-
1
(
2
x
+
1
)
3
2
=
-
1
(
2
x
+
1
)
2
x
+
1
(2)
u
=
-
x
2
とおくと、
y
=
e
u
y
'
=
e
u
×
d
u
d
x
=
e
-
x
2
×
(
-
2
x
)
=
-
2
x
e
-
x
2
(3)
(
f
×
g
)
'
=
f
'
×
g
+
f
×
g
'
だから、
f
(
x
)
=
x
2
,
g
(
x
)
=
log
x
として
y
'
=
2
x
×
log
x
+
x
2
×
1
x
=
2
x
log
x
+
x
(4)
u
=
cos
x
とおくと、
y
=
u
3
だから、
y
'
=
3
u
2
×
u
'
=
3
cos
2
x
×
(
-
sin
x
)
=
-
3
cos
2
x
sin
x

